Prior of the time of the telescope, man’s view of the celestial universe was woefully restricted when compared with what now can be enjoyed on any clear evening with ordinary binoculars. There were visible to him then only the naked-eye objects, the sun and the moon, five of the planets, and on a clear night stars down to about the 6th magnitude, some 2,000 in all. A few hazy spots could also be seen, and there would be an occasional comet. Completely unknown were the outer planets, satellites of the planets, Saturn’s rings, and infinite numbers of stars and galaxies.
Yet, working without optical aid, early observers managed to make some amazingly accurate charts of the visible stars, and amassed the observations from which the laws of planetary motion were deduced. The principal instrument used in establishing star and planet positions was the quadrant, a device having a graduated arc, and a pointer that pivoted about its center. With it Tycho Brahe (1546-1601), Danish astronomer, and one of the keenest of all observers, was able to record the positions of stars to within one minute of arc — about 1/30 the diameter of the moon. This was an amazing feat, when it is considered that one minute of arc is about the limit of visual acuity.
Then, in 608, seven years after Tycho’s death, the telescope was brought upon the scene by a Dutch spectacle maker, Jan Lippershey. to whom its invention is credited. The invention marked one of the great progressive triumphs of man, enabling him to reach farther and ever farther out into space. It was not much of a telescope, this first refractor, consisting of two spectacle lenses perhaps an inch in diameter, one convex and the other concave, and magnifying possibly two or three times. Lippershey, whose name historians spell in various ways, managed to combine two such instruments into a unit, and thus also made the first binocular telescope.
The Galilean Telescope
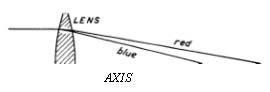
Very soon, spectacle makers and scientists up and down Europe, learning of Lippershey’s invention, were making similar instruments. Notable among the scientists was Galileo Galilei, the great Italian physicist and astronomer, who fitted a plano-convex and a plano-concave spectacle lens into opposite ends of a lead tube, making a telescope that magnified three times (Fig. 1). “They [the objects] appeared three times nearer and nine times larger in surface than to the naked eye,” wrote Galileo. He experimented further and improved this erecting telescope as well as was possible with simple lenses, carrying the magnification up to 30 or more. This was about the limit of its usefulness, however, on account of the great reduction in the size of its field of view.
The general arrangement of Galileo’s telescope is shown in Fig. 2. Ordinarily, rays from a distant object AB would, after refraction through the objective lens 0, meet to form an inverted image ba in the focal plane, but by interposing the concave eye lens E in front of that plane the rays are caused to become divergent, as though they had proceeded from the points A’B’, where a virtual image of the object is formed. This image is erect and magnified; the amount of magnification is the ratio of angle c’ to angle c.
 |
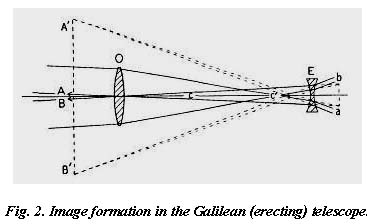As the eye pupil can hardly embrace all of the rays emerging from lens E, only part of the actual field shown can be utilized. Also, the exit pupil (explained in Chapter 13) is located inside the instrument. The field of view thus depends on the size of the eye pupil, and on the diameter of the objective lens. The Galilean telescope is found today in the form of opera and field glasses, but employing quite moderate magnification: 2 to 3 power in the opera glass, and 3 to 6 power in the field glass.
The Keplerian Telescope
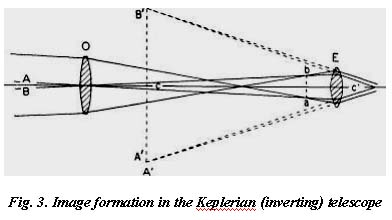
An improvement on Galileo’s telescope was made in 1611 by Johannes Kepler, a German astronomer and former pupil of Tycho, who suggested that the converging rays from the objective be allowed to come to a focus, and that the resultant image be magnified with a convex lens. Fig. 3 shows the advantage of this new arrangement. The rays, upon emergence from the eye lens, are now converging; hence more of them and a wider field of view can be taken in by the eye. Projected backward through the eye lens, the rays appear to proceed from B’A’, where a virtual image, inverted and enlarged, is formed. As before, the amount of magnification is in the ratio of angle c’ to angle c. Considerably higher magnification can be had with this inverting telescope.
 |
But with increasing magnification, the inherent defects of a lens, notably chromatic and spherical aberration (Figs. 4 and 5) were likewise increased. The aberrations could be diminished to a considerable extent by lengthening the focus of the objective lens. Consequently, in efforts to reduce these aberrations, enormous proportions were reached, instruments of 130 and 150 feet in length being constructed. Lens diameters up to six inches and more were attained. Non-spherical surfaces were also attempted in an endeavor to overcome spherical aberration. With these extremely long telescopes, working fields of only two or three minutes of arc must have been the rule. For comparison, the angular diameter of the planet Jupiter (at closest opposition) is almost one minute of arc, so the trials and patience of these 17th-century astronomers in aiming their exceedingly long instruments can be appreciated.
Magnification is a secondary consideration of the telescope; its chief function is to collect light. The eye alone gathers a limited amount of light, hence the luminosity of an object determines its visibility; also, the unaided eye can resolve only a limited amount of detail. An objective lens of the same diameter as the pupil of the eye would not improve vision, regardless of the amount of magnification employed, except that through this enlargement the detail in an object would be made more apparent. A 1-inch objective lens, assuming it to be about 3½ times the diameter of the eye pupil (about seven millimeters at night), collects about 13 times as much light, and correspondingly fainter objects become visible. The amount of detail seen is also increased, due to the greater aperture. So it is evident that the early observers needed larger objectives for greater light-gathering and resolving power.
|
|
But since spherical aberration increases with the square of the aperture, the only way in which it could be kept under control was to lengthen the focus, but there was a practical limit to what lengths could be handled. Moreover, a larger field of view was greatly desired, and this could accrue only with the use of shorter focal lengths. While spherical aberration could be pretty well eliminated by the use of two suitably curved lenses of the same kind of glass, there still remained chromatic aberration to be contended with.
|
|
In the hope of combining lenses of different glasses in such a way as to overcome chromatic aberration, Sir Isaac Newton attempted to determine if refraction and dispersion were the same in all optical media. Although his experiment was inconclusive, from it Newton assumed that refraction and dispersion were proportional to each other, and he decided that nothing could be done to improve the refractor. He therefore directed his energies to the formation of images from concave reflecting surfaces, which are perfectly achromatic.
The Gregorian Telescope
Practical experiments with reflectors had already begun in 1639, but it was not until 1663 that they gained any prominence. In that year a Scottish mathematician, James Gregory, at the age of 24, published a treatise entitled Optica Promota. In this he gave a description of a compound reflecting telescope employing two concave specula (metal mirrors). The larger one was to be perforated, and to have a paraboloidal surface; the smaller was to be ellipsoidal. The arrangement is shown in Fig. 6. Notice that the ellipsoidal mirror s is placed beyond the focal point F of the primary, which is also one of the foci of the ellipsoid. From this position, the secondary mirror returns the rays to form an erect image at its other focus f. High magnification could be had with this instrument, the second reflection amplifying the focal length of the primary in the ratio of fs to Fs. Construction of the telescope was undertaken, but whatever chance it may have had of performing creditably was lost by polishing the speculum on a cloth lap — putty (tin oxide) being used as the polishing agent. The unyielding lap was an insurmountable barrier to parabolizing, interest apparently ebbed, and about 60 years were to elapse before a workable model was finally produced.
The Cassegrainian Telescope
Sieur Cassegrain, a Frenchman, in 1672 designed a second compound reflector, differing from Gregory’s in that it employed a convex secondary, to be of hyperboloidal figure, placed inside of the focus of the paraboloidal primary (Fig. 7). The image formed at f in this case is inverted.
 |
The amplification from the second reflection is, as in the previous case, in the ratio of fs to Fs, and while the Gregorian is seen to be capable of higher magnification, all that is necessary can be had from the Cassegrainian, and it has the advantage of being a much more compact instrument. Although little was heard of this telescope for the next two centuries, it is worth observing that it survived the Gregorian, and is still widely used in observatories. The principal reason for its early lack of popularity was no doubt due to the difficulty of giving a hyperboloidal figure to the secondary mirror. This difficulty can be avoided by leaving the secondary with a spherical figure and undercorrecting the primary. It is also possible to leave the primary spherical, and to make all the correction at the center of the secondary, which will then have an oblate spheroidal form.
 |
The Newtonian Telescope
In the same year, Newton designed and constructed two small reflectors, of the type so popular with amateur astronomers today and which still bears his name. They were not large, as we know telescopes today, the effective apertures of the concave specula being about 1 1/3″. Their focal length was 6″, making the focal ratio f/4.5. To bring the light rays to a convenient place for observation, a plane speculum was used for the secondary reflection. This was placed at a 45° angle a short distance inside the focus of the primary, where it could deflect the rays out through an opening in the side of the tube. There the inverted image was magnified with a plano-convex eyepiece of about 1/6″ focal length, giving a total magnification of about 36 diameters.
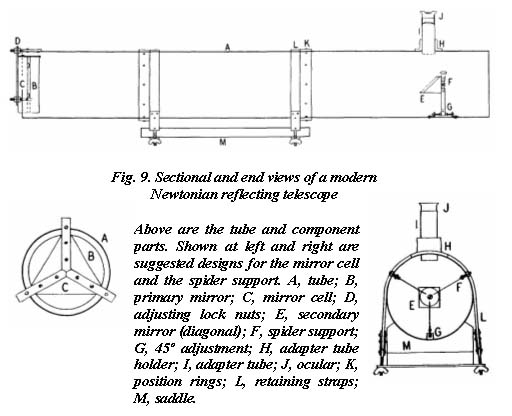
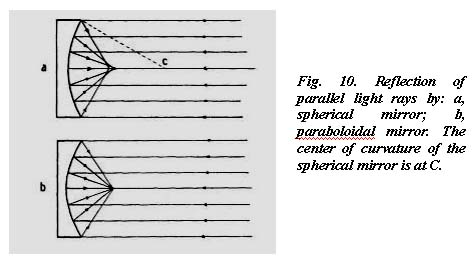
The plan of a modern Newtonian is shown in Fig. 9, and the reflection of rays in Fig. 47. As with the compound telescopes, the primary mirror must be a paraboloid, since a spherical surface cannot reflect parallel rays, such as those from a star, to a single focus. This is shown in Fig. 10a, where rays striking the edge zones of a spherical mirror are brought to focus inside the focal point of the central-zone rays. The paraboloid (Fig. 10b) is the only surface that can bring parallel rays to a single focus.
 |
Newton, according to his Opticks (1704), polished his specula on pitch, using putty as the polishing agent. His methods were ingeniously calculated to yield a spherical surface, and it is quite probable that a close approach to that figure was attained. But the performance of even a spherical mirror of the proportions of Newton’s could hardly be satisfactory because of the great amount of spherical aberration present. Although Newton thought that his mirror might fail of good definition, he “despaired of doing the work” (parabolizing the speculum), yet he “doubted not but that the thing might in some measure be accomplished by mechanical devices.”
Referring back to Fig. 10a, it might be concluded from a study of the diagram that if the center of the mirror were properly deepened, that is, given a shorter radius, or if the radii of the outer zones were progressively lengthened, or if a little of each were done, all the reflected rays could be brought to a common focus.
 |
That is a practical solution, and the resulting surface in each instance is a paraboloid. The standard practice is to deepen the spherical mirror so that, for a 6-inch f/8 mirror, the making of which is described in this book, the glass removed in the operation is but half a wave length of light in thickness at the center. Incredible though it seems, this represents the difference between poor and good definition.
 |
The single-lens eyepiece of Kepler’s had already been improved, with the addition of another element, by Christian Huygens, a Dutch astronomer and mathematician, about the year 1650. His compound eyepiece is shown in Fig. 68. The field lens, like Galileo’s concave lens, is placed before the focal plane of the objective. As it is convex, however, it further converges the rays to form’ a slightly smaller image in a new focal plane, which is then magnified by the eye lens. Thus, a much wider field of view is encompassed by the eyepiece.
Further Developments
In 1722, John Hadley, an English mathematician, completed a Newtonian form of reflector (Fig. 11), in which the mirror evidently was suitably figured. It was about 5I/2″ in diameter, and 62%” in focal length. With a mirror of these dimensions, practically perfect definition could be realized if the surface was given a spherical figure. (See the discussion on surface tolerance in Chapter 7.) This instrument attracted considerable attention, and presently other makers were turning out Newtonian reflectors, following Hadley’s technique, which consisted of removing the spherical aberration as it was revealed by the extra-focal diffraction rings of a star image.
Hadley then turned his attention to Gregory’s design, and in 1726 he produced an instrument slightly over 2″ in diameter and 12″ in focal length. This proved so successful that construction was undertaken by other opticians, or artists, as instrument makers and craftsmen appear to have been then known. Notable among these was James Short, who made both Newtonians and Gregorians in great numbers, from about 1732 to the time of his death in 1768. Observatories purchased his larger instruments, a tribute to his skill, and the smaller ones were marketed chiefly among the aristocracy and those amateur astronomers of the day who could afford them.
The principal attraction of the Gregorian design was the erect image it gave, which made it suitable for terrestrial use. This circumstance influenced its preference over the Newtonian, notwithstanding the fact that its images must have been pretty dull. Well into the 19th century, however, the Gregorian rode a wave of popularity that no type of telescope has known, until overwhelmed in comparatively recent years by the flood of amateurs who have Hocked to Newton’s design.
From the time of the invention of the telescope, and the startling discoveries of Jupiter’s moons and the rings of Saturn, interest in astronomy had become something infectious. Each new discovery was accorded the widest publicity, stimulating a desire among those of learning to gain at first hand a glimpse of these celestial wonders. It was not practicable as yet for the average individual to make his own speculum, but many contrived to fit spectacle lenses into tubes, much as Galileo had done some 150 years earlier. Those whose means permitted bought telescopes, and envied was the gentleman who possessed one of three or four inches aperture, by an “exclusive” artist. But, judged by present-day standards, many of those reflectors were tiny. There is one (maker unknown) in the Fugger Collection at Augsburg, barely 1″ in diameter and 6″ in focal length, that was concealed in a walking stick! Eyepiece lenses of 1/6″ or less in focal length were quite common.
 |
The metal used in those early mirrors was an alloy of copper and tin, the usual proportion about 75 to 25, which could be given a beautiful polish. But the metal was extremely hard to work, and a prodigious amount of labor was involved in grinding and polishing the curve. To facilitate the work, the comparatively thin disks were cast to the approximate curve, the backs also being curved to give uniform thickness and equalization of temperature effects. Grinding was done on convex iron tools of similar radius, using emery, and sometimes sand. Polishing was done on a pitch lap, with rouge. Manufacturers usually devised their own machines to do the work of grinding and polishing. Except where the utmost perfection was imperative, figuring seems to have consisted for the most part of a final brief variation of the stroke, in an unguided attempt to concentrate the polishing at the center. Critical testing, undoubtedly seldom indulged in on account of its laboriousness, could as yet only be performed on a star. In reflective ability, speculum was only about 60 per cent efficient, and the surface tarnished rapidly, effecting a further serious light loss. This meant frequent repolishing, and repolishing meant refiguring.
It is interesting to inquire into the prices that were asked for telescopes in that period, the latter half of the 18th century. Listed below are prices and sizes of a few of the Gregorians made by Short, selected from his catalogue. Newtonians in similar sizes were priced only slightly lower.
|
Diameter (inches) |
Focal Length (inches) |
Magnification |
Price (guineas) |
|
1.1 |
3 |
18 |
3 |
|
1.9 |
7 |
40 |
6 |
|
4.5 |
24 |
90-300 |
35 |
|
6.3 |
36 |
100-400 |
75 |
|
18 |
144 |
300-1,200 |
800 |
By the beginning of the 19th century, amateurs were able to procure specula for the primary and secondary mirrors, for both Newtonian and Gregorian designs. These could be had finished, ready for mounting, or as rough blanks to be ground and polished, not at the amateur’s discretion, but to the curve of the iron tools furnished by the maker. Of course, the amateur had no means of correcting the figures of his mirrors, or even of knowing what they might be, the one reliable method of testing not being common knowledge.